建物の揺れというのはなかなか複雑なもので、簡単に理解することはできません。また、完全に解明されているわけでもなく、今後も研究が続けられていくでしょう。
しかし、わかっていることもたくさんあります。力学モデルを構築してさまざまな解析を行ったり、地震被害の実地調査を行ったりして得られた知見がそれです。
その中でもまずは知っておきたい基本的な知識として「固有周期」があります。建物の揺れ方を決める重要な指標ですので、しっかりと理解していただきたいものです。
基礎の部分から実務的な部分まで、一般の方にもわかるように説明してみます。
固有周期とは何か
「建物の固有周期」とは「その建物が揺れるとき、揺れが一往復するのにかかる時間」のことです。
具体的に言うと、ある建物を元の位置から右側にグッと押してから手を離した場合、
① 右側から元の位置に戻ろうとする
② 元の位置を通過するが勢い余って左側に振れる
③ 左側から元の位置に戻ろうとする
④ 元の位置を通過するが勢い余って右側に振れる
⑤ 右側まで戻る
⑥ ①~⑤を繰り返す
上記「右⇒元⇒左⇒元⇒右」という①~⑤の一連の動きに要する時間です。
固有周期の求め方
何で決まる?
固有周期は建物の「重さ」と「硬さ」の関係で決まります。もう少し専門的に言うと「質量」と「剛性」の関係です。
前述のように、固有周期とは往復するのにかかる時間ですから、早く動ければ短くなりますし、遅くしか動けなければ長くなります。つまり、その建物が素早く動けるかどうかを表している値だと考えることができます。
例えば、重い荷物を持たされると人は素早く動けません。建物も同じです。軽ければ早く、重ければ遅い、というのは感覚的にも分かると思います。
しかし、同じ重さの荷物を持っているからと言って同じ動きになるとは限りません。力の強い人と弱い人とでも違います。力が強ければ少しくらい重くても苦にならず早く動けます。
人にとっての「荷物」と「力の強さ」が、建物にとっての「重さ」と「硬さ」というわけです。
公式(単位に注意)
固有周期は以下の公式により求めることができます。
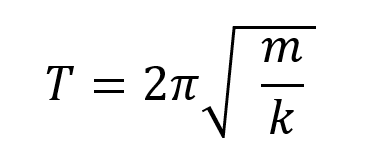
T:固有周期(秒)、m:質量(ton)、k:剛性(kN/m)です。単位が重要ですので、間違えないようにしましょう。
質量が大きいほど、つまり建物が重いほど周期は長く(ゆっくり動く)なり、逆に剛性が大きいほど、つまり建物が硬いほど周期は短く(素早く動く)なります。
「4tonのおもり」を「100kN/mのばね」に吊るして上下に揺らすときの周期は
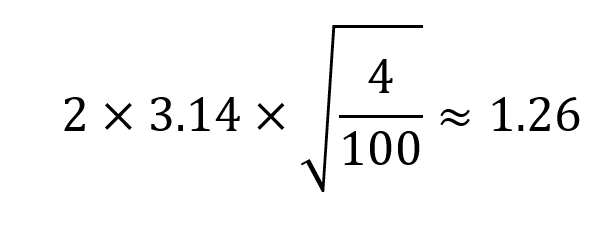
ということで、大体1.26秒になります。
ちなみに、「おもりを吊るしたときに25cm伸びると周期は約1.0秒」というのは知っていると便利です。先ほどの例では約39.2cm(=4×9.8)伸びますので、39.2/25の平方根を取ると1.25秒という近い数値が出ます。
なぜ平方根か
先ほどの公式の中に「√」があるのが気になった人もいるかもしれません。重さが倍になれば動く速さは2倍になりそうなものですが、周期はその平方根である1.4倍程度しか長くならないということです。
数式を解くと確かにそうなっていることは確認できますが、物理的にどういう意味を持っているかは理解できません。ここではあまり数式を使わずに説明してみます。
周期を半分にする場合を考えてみましょう。
まず、周期を半分にするには、建物の揺れる速さを2倍にする必要があります。単純ですね。
しかし、周期が半分ということは、加速に使える時間も半分しかないということです。半分の時間しかないのに速度を2倍にしなくてはならないので、加速度は4倍にする必要があります。
ma = F、つまり「質量×加速度=力」ですから「加速度=力/質量」です。加速度を4倍するには発揮する力(硬さ)を4倍にするか質量(重さ)を1/4倍しなくてはならないことがわかります。
なるほどと思っていただけたでしょうか。
建物の揺れ方と共振
建物は一棟一棟、重さも違えば硬さも違います。階数も違えば広さも形も違います。これらの建物の揺れ方を比較するにはなにか基準となるものが必要ですが、それが固有周期です。
超高層ビルだろうが平屋建てだろうが、固有周期さえ同じであれば基本的な揺れ方は同じだからです。固有周期以外にも揺れ方に影響を与えるものはあるので完全には一致しませんが、少なくとも大体の傾向はつかめます。
固有周期の影響が最も大きく出るのが「共振」です。建物と地震の周期が一致する現象のことです。
通常、地震のエネルギーが損失無くすべて建物に入力されることはありません。建物が右に揺れているのに地面からは左に揺らそうとする力がくることもあり、力が相殺されて揺れは弱まります。
しかし共振の場合、常に揺れを増幅するようなタイミングで建物と地面が動いてしまい、時間の経過とともにどんどん揺れが大きくなってしまいます。
固有周期が近い建物同士は同じような地震と共振を起こすため、地震時の被害の状況も似通ってくることになります。
高さと構造種別(木造・鉄骨造・RC造)
建物の設計は建築基準法を満足するよう行われますが、確認項目の一つに建物の「変形」があります。地震のときに建物にかかる「力」と建物の「硬さ」から、建物の変形が許容値に納まるかを検討します。
このとき、力は「重さ」に係数を掛けて求めるので、結局「重さ」と「硬さ」の関係を法律で規定していることになります。固有周期とはまさに「重さ」と「硬さ」で決まりますから、法律に則って設計すると「固有周期は大体これくらいになる」という範囲があることになります。
それがこの略算式です。
![]()
T:固有周期(秒)、h:建物の高さ(m)、α:木造か鉄骨造の階の高さの割合です。
要するに、鉄筋コンクリート造(RC造)、鉄骨鉄筋コンクリート造(SRC造)だと
![]()
鉄骨造(S造)、木造だと
![]()
となります。
高さ200mの鉄骨造のオフィスビルだと固有周期は6.0秒(=200×0.03)、高さ120mのRC造のタワーマンションだと固有周期は2.4秒(=120×0.02)くらいになるということです。
ただ、実際にはかなりばらつきがあります。特に低層建物で顕著です。
まず、法律の規定よりも余裕を持たせている、変形制限ではなく別の要因で決まっている、というような設計に起因する部分があります。
構造形式による差もあります。高層建物は柱と梁だけで地震に抵抗する「ラーメン構造」を採用することが多いですが、低層建物は「ブレース構造」や「壁式構造」というような硬めの構造形式が増えます。すると周期は略算式の値よりも短めになります。
また、間仕切壁や外装材など、計算上は見込んでいないけれど実際には硬さに寄与するものが付いています。特に木造住宅などではこの影響が顕著です。
免震構造と地盤・地震の周期
過去に観測された地震動を分析してみると、周期が短い建物ほど強く揺すられることがわかります。また、被害が大きかった地震では周期1~2秒程度の「キラーパルス」と呼ばれる成分が多いことが知られています。
地震時に地面がどう揺れるかは断層の壊れ方や、建物が建っている地域の地盤の影響を受けます。しかし、どうやら周期4秒くらいの成分は大きくないことがわかっています。
「4秒よりも固有周期が長い建物は地震のとき強く揺すられないだろう」という考えのもと、あえて固有周期を長くした建物が「免震建物」です。そのため、免震建物は固有周期4秒以上としていることが大半です。
最近は4秒よりも周期の長い揺れの発生も危惧されており、設計時には考慮することになっています。
「固有」だけど「固有」じゃない
「固有」には「もともと備わっているもの」「それだけにあるもの」という意味があります。そのため固有周期は一定で不変のものと思ってしまいがちですが、実際は違います。
地震の最中に建物の重さが変わることは基本的に無いですが、硬さが変わることはしょっちゅうです。地震で建物が変形するとひび割れが入ったり、壁が緩んだりと柔らかくなっていきます。
固有周期は「重さ」と「硬さ」の関係ですから、重さが変わらずに柔らかくなっていけば固有周期は長くなります。特にコンクリート造の建物では地震後に固有周期が長くなったという事例がいくつもあります。
また、固有周期は建物ごとに一つではありません。いくつもあります。
例えば、南北方向、東西方向、ねじれ方向の揺れを考えれば3つです。さらにそれぞれ「1階と2階が逆に動く場合」と「同じ方向に動く場合」など、考え出すとそれこそ本当にたくさんあります。
あくまでも略算式で求められる固有周期は代表的な値の1つです。本来はちゃんと解析していろいろな固有周期を把握しなくてはなりません。
等価周期
通常、固有周期と言えば建物が損傷していない初期の状態での周期を指します。しかし、建物が大体どのくらい揺れるか、そしてそのときどのくらい損傷するかがわかっていれば、その状態での固有周期を知っておくことには意味があります。この「ある程度壊れてきた状態での周期」を「等価周期」といいます。
最初は1cm変形させるのに8kNの力が必要だったものが、変形させるにつれて柔らかくなっていき、8cm変形させるのに16kNしか必要なくなったとします。もし最初の硬さのままであれば64kNとなるところが、その1/4で済みました。
固有周期は硬さの平方根に反比例しますので、硬さが1/4なら周期は初期の2倍に伸びます。これが8cm変形時の等価周期となります。
固有振動数
固有周期の逆数を「固有振動数」といいます。
固有周期は「揺れが往復するのにかかる時間」でしたが、固有振動数は「1秒間に揺れる回数」です。
別にどちらの値を使ってもいいのですが、建物の揺れに対しては固有周期を使うことが多いです。自分で揺れるものの場合は固有振動数、誰かに揺すられるものの場合は固有周期、というような使い分けで大体良いかと思います。