地震の揺れを観測するため、日本中に地震計が設けられています。地震計位置における加速度データは記録され、耐震工学の発展をはじめ、いろいろなことに使用されています。
しかし、その記録された地震波のデータを見ただけではほとんど何もわかりません。せいぜいが継続時間や最大加速度くらいでしょう。データをうまく処理することで、知りたい情報を読み取らなくてはなりません。
例えば、地震によってどの程度の被害が出たかを推測するのに「震度」が役立ちます。被害状況を反映できるよう、観測された地震波のデータを処理して導かれるからです。
震度が地震の強さを表すわかりやすい指標と一般には考えられていますが、構造設計者にとってはそうではありません。「震度7でも倒れませんか」と聞かれても、実は何も答えられないのです。
地震が持つ様々な特性を表すのに、1つの指標だけでは十分ではありません。震度だけではほとんど何もわからないのと同じです。ただ、そんな中でもかなり多くの情報を得ることができる指標があります。それが「応答スペクトル」です。
応答スペクトルとは
できるだけ短く答えるなら、「ある地震動に対する1自由度系の最大応答値を時刻歴応答解析により求め、固有周期ごとにプロットしたもの」と言えるでしょう。もちろんこれでは全くわかりませんね。順を追って説明していきます。
1自由度系:建物の揺れを単純化
建物の揺れとは、それほど単純なものではありません。建物全体が右に、あるいは左に揺れる、つまり建物が『/』のように揺れる場合だけでなく、『く』や『S』のようにクネクネと揺れる場合もあります。
2階建てであれば『/』と『く』だけ考えれば問題ありませんが、超高層ビルになると『S』どころか『ξ』でも足りないかもしれません。当然、考慮しなくてはならない揺れ方が増えるほど複雑になっていきます。
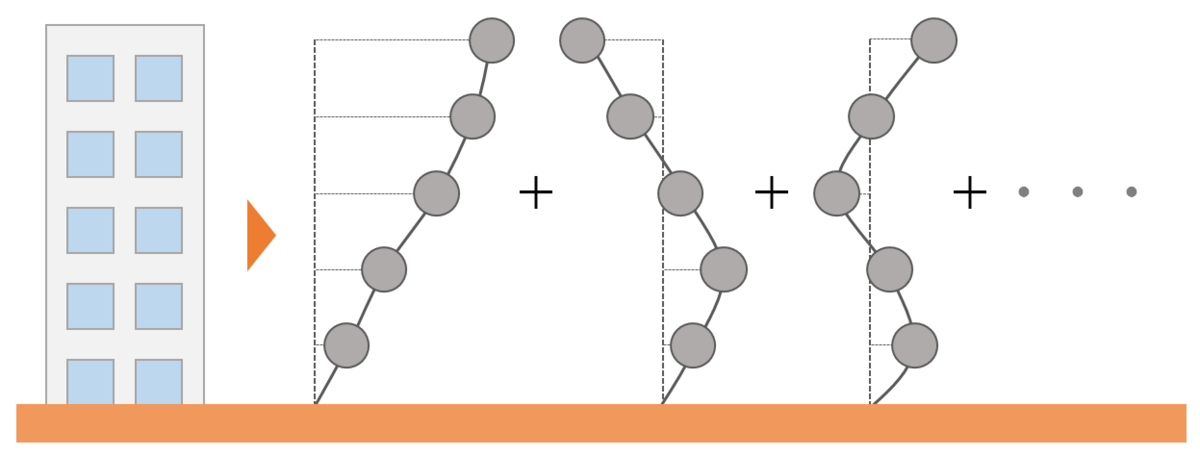
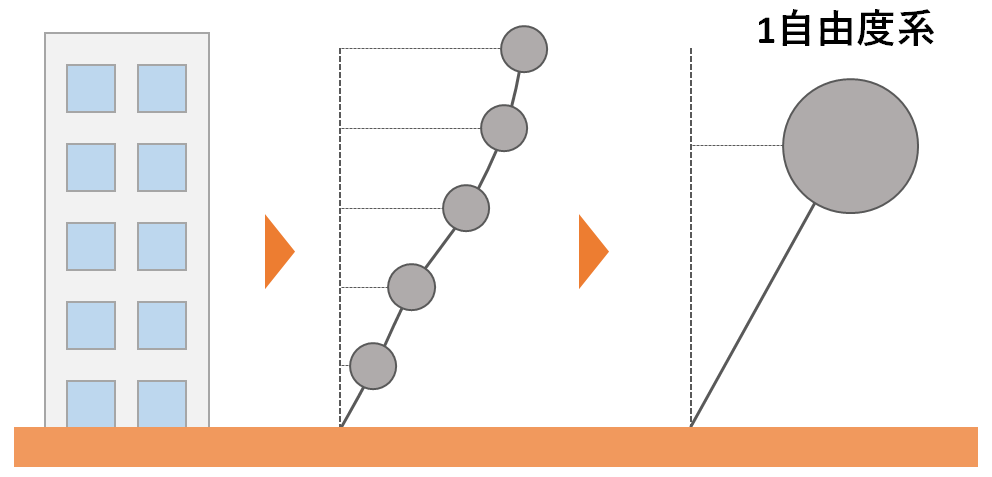
しかし、今知りたいのは地震の特性です。地震の特性を大掴みするのに、複雑な建物モデルを考える必要はありません。そこで、『く』や『S』を無視して、『/』だけを取り出して考えます。
『/』ということは、右に○cm変形した、あるいは左に△cm変形したというように1つの数字で揺れの状態を表せるということです。この単純なモデルを「1自由度系」と言います。単純な分、計算が簡単になります。
固有周期:建物の揺れ方の特性
建物にはそれぞれ固有の揺れ方があります。硬くて軽い建物は速く、柔らかくて重い建物はゆっくり揺れます。低層の建物であればガタガタと素早く、超高層ビルではグ~ラグ~ラとゆっくり揺れるのが想像できるかと思います。
右に揺れ、次に左に揺れ、そして元の位置に戻ってくる、この一連の動きに要する時間を「固有周期」と言います。固有周期は建物高さに概ね比例するので、固有周期が何秒かが分かれば大体何階建ての建物かがわかることになります。
一般的に、建物高さ(m)に0.02~0.03を乗じたものが固有周期(秒)です。100mくらいの高さであれば、2~3秒程度になるということです。階高を4mとすれば25階建てですから、階数に0.1を乗じたものが固有周期(秒)になるとも言えます。
固有周期だけで地震時の建物の揺れ方の全てが決まるわけではありません。ただ、固有周期が同じであれば、かなり似たような揺れ方をします。逆に言うと、固有周期が違えば建物に生じる揺れは全く違うものになります。
そのため、「固有周期が○○秒の建物はこれくらい揺れる、△△秒の建物はこれくらい揺れる」というように、地震の特性を知るには建物の固有周期ごとに分けて考える必要があるのです。
時刻歴応答解析:地震時の建物の揺れを計算
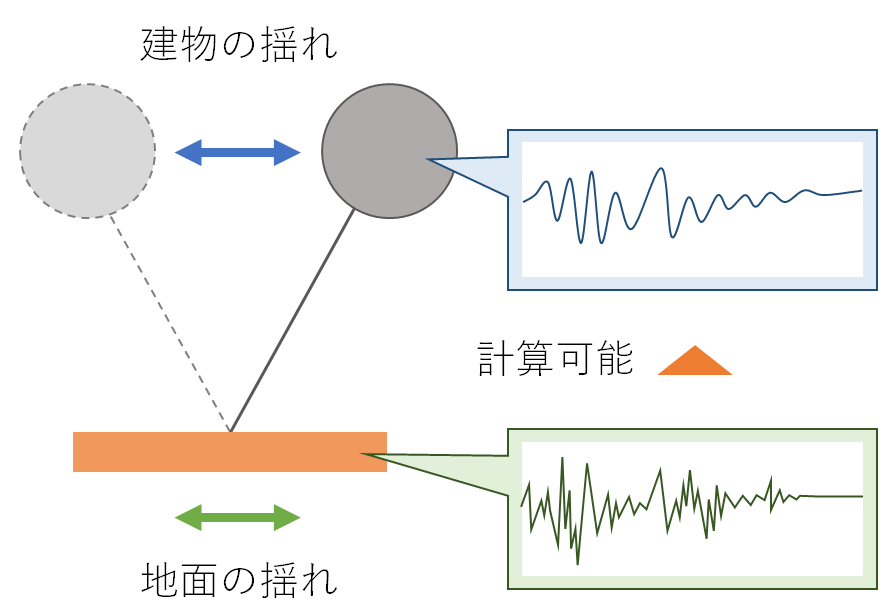
地震とはガタガタと地面が揺れる「動的」な事象なので、「この式を使って1回計算すればわかる」というものではありません。「0.01~0.02秒の間はこう揺れて、0.02~0.03秒の間はこう揺れる」というように、非常に短い時間ごとに計算を繰り返さなくてはなりません。
建物の各時刻での揺れと、地面の動きを用いて順次計算を行うことで建物の揺れを求める解析を「時刻歴応答解析」といいます。
毎回の計算自体も大変ですが、地震の継続時間は数十秒はあるので、とんでもない回数の計算を繰り返す必要があります。電卓ではほぼ対応不可能で、専用の解析ソフトを用いて行うことになります。
しかしこの計算を行うことで、地震時の建物の揺れが地震の発生から終了までを通してわかるのです。
最大応答値:設計に必要な値
当然ながら、地震が起こっている間、建物に生じる揺れは刻々と変化します。揺れが大きい時間もあれば、小さい時間もあります。
5mmの変形が20回続くのと10mmの変形が1回生じるのとでは、どちらが建物に与える損傷が大きくなるかはわかりません。ただ、5mmが1回よりも10mmが1回の方が厳しいのは明らかです。
一般的な構造計算では、変形が繰り返すことによる損傷の効果を見込んでいません。そのため、最大値がいくらになるかが最大の関心事になります。
長周期地震動のように長時間継続するのでなければ、最大値を押さえておけば設計としては問題無いのです。
つまり応答スペクトルとは
ここまで読んでいただければ、最初に示した説明も理解できるようになっているはずです。
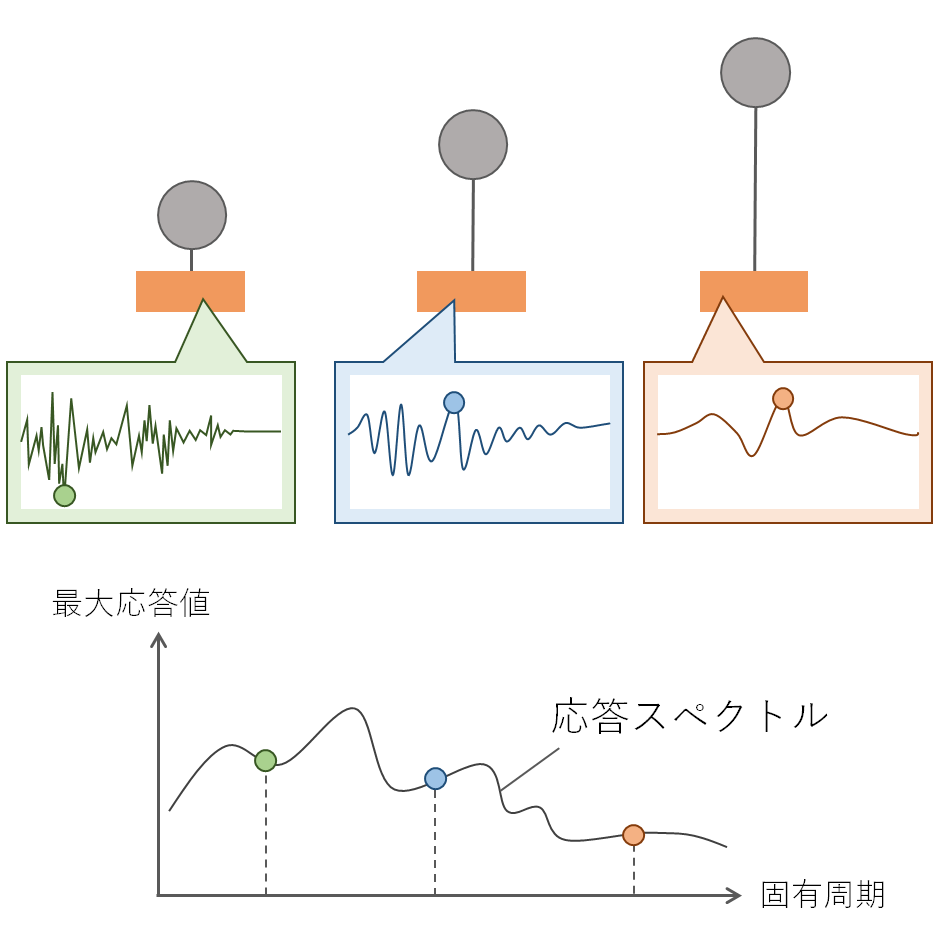
つまり応答スペクトルとは、①建物を単純化した1自由度系のモデルを用いて、②モデルの固有周期をいろいろ変化させて、③地震波のデータを用いて時刻歴応答解析を行い、④最大応答値を抜き出し、⑤縦軸に最大応答値、横軸に固有周期をプロットしたもの、です。
時刻歴応答解析は通常の解析よりは時間がかかります。ただ、計算対象となるモデルが単純なため、応答スペクトルの作図は比較的簡単にできます。
建物の高さが分かれば大体の固有周期は分かります。固有周期がわかれば、わざわざ解析しなくても応答スペクトルから揺れの最大値がわかるのです。
変位・速度・加速度
建物の揺れの状態は変位、速度、加速度の3つがあります。どれも大切な指標で、それぞれ変位応答スペクトル、速度応答スペクトル、加速度応答スペクトルによって最大値を知ることができます。
建物に生じる変位は、建物の損傷に密接に関係しています。損傷を抑えるには建物の変位を小さくする必要があります。固有周期が長いほど大きくなる傾向にあります。
建物に生じる速度は、建物に入力されるエネルギーと考えることができます。大きな速度が生じるということは、それだけ建物を揺らす地震のエネルギーが大きいことになります。固有周期が長くなると一定になる傾向にあります。
建物に生じる加速度は、地震の力の大きさです。建物の重さに加速度を掛けたものが力になるからです。固有周期が長いほど小さくなる傾向にあります。
下の図は、1995年の兵庫県南部地震において、神戸海洋気象台で観測された地震動の応答スペクトルです。

変位や速度は「地面と建物の動きの差」が重要になる相対的なものです。地面と建物の動きが同じであれば、建物に生じる変位や速度はゼロになります。
加速度は「地面と建物の動きの和」が重要になる絶対的なものです。地面が右に加速しても、その分だけ建物が左に加速すれば力は生じないのです。
そのため、変位と速度の応答スペクトルは「相対系」、加速度の応答スペクトルは「絶対系」で描かれる場合が大半です。
疑似応答スペクトル・トリパタイト
時刻歴応答解析を行えば、変位、速度、加速度の全て値が分かります。そのため、それぞれに対応した応答スペクトル、つまり3つの応答スペクトルを描くことができます。
それはそれで便利なのですが、実はこの3つの図を1つにまとめることができるのです。1つの図で3つの情報が得られるようになる、これはさらに便利です。
変位、速度、加速度にはそれぞれ関連があります。変位の変化率が速度、速度の変化率が加速度です。完全に独立しているわけではありません。
この関係を利用することで図をまとめることができます。しかし一点注意が必要です。それは変位と速度は「相対系」なのに対し、加速度は「絶対系」なことです。
本来は相対系か絶対系、どちらかに統一しなくてはいけません。しかし、相対系と絶対系が混在した状態でも、それなりの精度を持ちます。地震の特性を理解するのには支障ありません。
この図は縦、横、斜め×2の計4軸を有する図になります。横軸は固有周期、縦軸は速度になっており、本質的には速度応答スペクトルです。
しかし時刻歴応答解析から直接求めた値ではなく加速度応答スペクトルから求めた値なので「疑似速度応答スペクトル」と呼ばれます。また、一度に3つの値を読み取れるので「トリパタイト」とも呼ばれます。