地震が起こったり、風が吹いたり、あるいは人がぶつかったりするとモノが揺れます。しかし、いつまでも揺れているわけではありません。いつかは揺れが収まります。
揺れが収まるのは「減衰」があるからです。「減衰」とはモノが振動するエネルギーを吸収・発散し、時間の経過とともに揺れを小さくしていく効果のことです。
モノの揺れ方を決めるのは「重さ」と「硬さ」ですが、揺れにくさを決めるのは「減衰」です。減衰を知らずして振動のことはわかりません。
減衰には分かりにくい用語が出てきますが、「減衰係数」と「減衰定数」というこのふたつの似た言葉が最たるものでしょう。できるだけわかりやすく説明してみます。
減衰係数(粘性減衰係数)とは
速度に比例して力を発揮する
モノの振動の状態は「加速度」「速度」「変位」で表されます。建物に力が加わることで揺れが生じるわけですが、この「加速度」「速度」「変位」と力はどのような関係にあるのでしょうか。
まず、「加速度」とは「速度の変化率」です。速度が急激に変化する、つまり急発進、急ブレーキをすると大きな「加速度」が生じます。「重さ」×「加速度」がモノに生じる力になります。
次に、「変位」とは「元々の場所から動いた距離」のことです。「硬さ」×「変位」がモノに生じる力になります。
最後の「速度」は特に説明不要でしょうが、「物体が動く速さ」のことです。では「速度」がモノに生じさせる力は一体何に比例するのでしょうか。ここで出てくるのが減衰です。「減衰係数」×「速度」がモノに生じる力になります。
「減衰係数」とは「物体の動く速さに応じて生じる力を表す係数」ということができます。これだけではなんだかよくわからないかもしれませんが、「重さ」や「硬さ」と同様にモノの揺れ方に影響を与えるもの、と認識してください。
「重さ」と「硬さ」とは違うタイミングで力を発揮する
モノが揺れる際、「変位」が最大になったとき「硬さ」による力が最大になります。変形したモノを強く元の位置に戻そうとするためです。
実は、「変位」が最大に達したときに「加速度」も最大になります。今まで右方向(または左方向)に向かって動いていたものが、方向転換をして左方向(または右方向)に向かって動き出そうとするため、速度の変化率、つまり加速度が大きくなるのです。そのため「重さ」による力が最大になります。
では「速度」はどうでしょうか。方向転換をしようとするということは、瞬間的に止まるということです。つまり速度はゼロになります。そのため「減衰係数」による力もゼロになります。逆に「変位」がゼロの時「速度」は最高になり、「減衰係数」による力が最大になります。「重さ」や「硬さ」とは力を発揮するタイミングが違うことがわかります。
ブランコで考えてみるとわかりやすいかもしれません。ブランコが一番高い位置に来ると一瞬ピタッと止まります。そのあと下に下がりながら速度を増し、一番低い位置で速度が最高に達します。その後また上に上がるにつれて速度が低下し、再び止まります。モノの揺れも基本はこれと同じです。
揺れのエネルギーを蓄え、それを変位が最大になると同時に開放するのが「加速度」と「変位」に比例する「重さ」と「硬さ」による力です。これは揺れを「継続」させようとする力になります。
「速度」に比例する「減衰係数」による力は真逆のタイミングで作用します。そのため、揺れを「停止」させようとする力になります。
揺れを止めようとする力がどのくらいか、というのを表す値が「減衰係数」です。
ダンパーの性能を表す
モノの揺れを止める装置といえば制振ダンパーがあります。制振ダンパーを設置することで「減衰を付加する」ことができ、揺れが収まるのを早めたり、モノに生じる変形を小さくしたりできます。
粘弾性ダンパー、粘性ダンパー、オイルダンパーのように「速度」に応じて力を発揮するタイプのダンパーでは、性能を表す値として「減衰係数」が使用されます。「減衰係数」が大きいか小さいかで、そのダンパーがどの程度揺れを抑えることができるのかがわかります。
減衰定数(粘性減衰定数)とは
読み方
「減衰係数」とよく似た言葉として「減衰定数」があります。
「げんすいていすう」または「げんすいじょうすう」と呼びますが、専門家は「げんすいじょうすう」と呼ぶことが多いように思います。
臨界減衰
減衰が大きければ大きいほど揺れがすぐに収まるわけですが、極端に減衰が大きい場合はなにが起こるでしょうか。通常は右、左、右、左、・・・と繰り返しながら徐々に振れ幅が小さくなっていくわけですが、減衰がある値を超えると一往復する間もなく、そのままゆっくりと止まってしまいます。
これを「過減衰(かげんすい)」と言い、減衰が大き過ぎて振動しない状態を指します。
この過減衰になるかどうかというギリギリの減衰を「臨界減衰(りんかいげんすい)」といいます。これよりも減衰が小さければ普通に振動する状態、これよりも減衰が大きければ振動しない状態になります。
この「臨界減衰」の状態を「減衰定数=1(=100%)」としています。
つまり、「減衰定数<1」では普通に振動し、「減衰定数≧1」では振動せずにゆっくり停止しようとする、ということです。
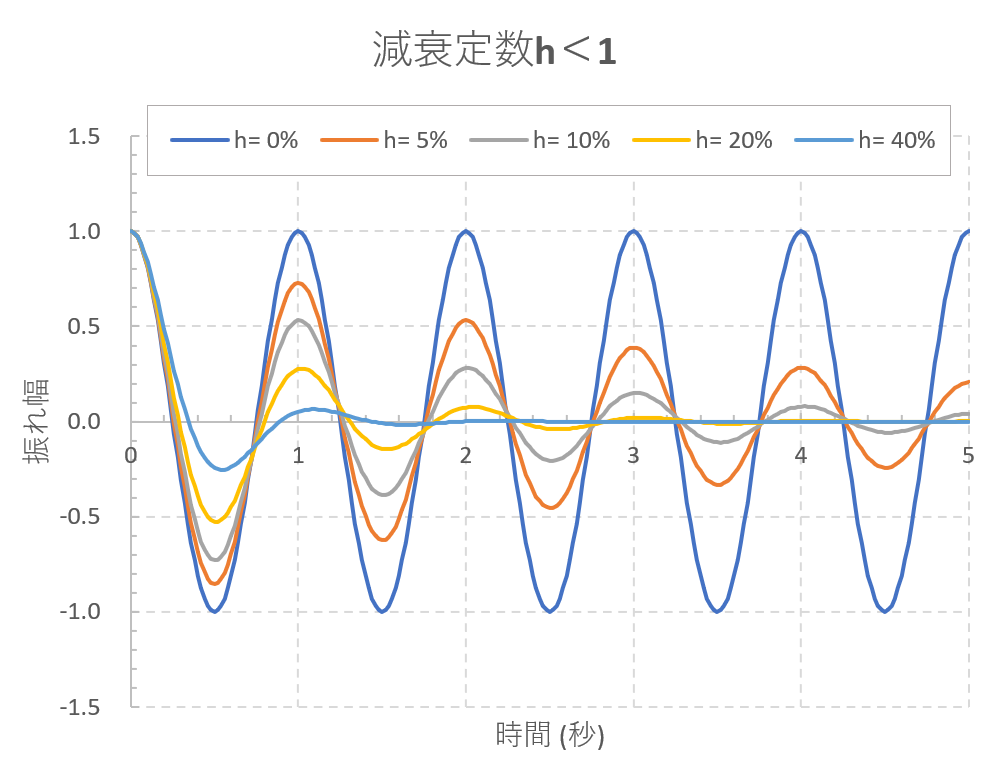
周期1秒の振り子を揺すった時の振れ幅の変化を減衰定数ごとに書いたものが下の図です。減衰定数<1の範囲では減衰定数が大きいほど揺れが収まるのが早いことがわかります。減衰定数≧1の範囲では振動しないので、減衰定数が大きいほど元の位置に戻るのに時間がかかるようになります。

減衰の単位:減衰係数は単位あり、減衰定数はただの比率
減衰係数は速度に応じてどれくらいの力を発揮するかという値です。そのため、力を速度で割った単位(例えば、kN・s/m、N/kine、etc.)を有しています。
それに対し減衰定数は、臨界減衰との大小関係を比べたものなので単位がありません。ですので、単に0.04と書いたり、「%」をつけて4%と書いたりします。
同じ周期の振り子が2つあるとき、減衰定数の大小関係は直接比較することができます。「Aが減衰定数3%でBが減衰定数2%であれば、Aの方が早く揺れが収まる」と言えます。
しかし減衰係数ではそうはいきません。同じ減衰係数のダンパーを設置する場合でも、振り子の重さが違えば意味が変わってきます。100tの振り子にダンパーを1台設置するのと、5kgの振り子にダンパーを1台設置するのでは効果が全く違う、ということです。
減衰係数はダンパー1台の性能、減衰定数は振動するモノ全体の性能と言ってもいいかもしれません。
減衰の計算・求め方
モノの揺れ方は「重さ」と「硬さ」と「減衰」で決まるので、この3つが決まれば減衰定数も決まります。一番単純なモデルである「オモリ1つ、ばね1つ」の場合は下の式で計算できます。

ここで
h:減衰定数、c:減衰係数(kNs/m)、k:硬さ(kN/m)、m:質量(ton)
T:固有周期(秒)、ω:固有円振動数(rad/s)
また、直接これらの値がわからなくても、揺れ幅が一往復するたびにどれだけ小さくなっていくかの比率からも求めることができます。