モールの定理による梁のたわみの計算例

梁のたわみを求める方法はいくつかあります。全て解析ソフトが計算してくれる時代ではありますが、電卓1つでできることもまだまだ多いです。

ここでは「モールの定理」を用いて、片持ち梁と単純梁に集中荷重と等分布荷重が作用したときの曲げによるたわみ量と回転角の計算を行います。

片持ち梁先端に集中荷重が作用する場合

①：長さlの片持ち梁の先端に集中荷重Pが作用しています。梁は一様断面で、ヤング係数および断面二次モーメントはそれぞれE、Iとします。

②：曲げモーメントは直線状に変化し、根元で最大のPlになります。

③：モールの定理に従って、左側の自由端を固定端に、右側の固定端を自由端に、モーメント分布を上下ひっくり返しEIで除して分布荷重に置き換えます。

④：分布荷重の面積を計算して集中荷重Pl²/2EIに置き換えます。作用位置は三角形の重心位置です。

⑤：このときの固定端のせん断力が片持ち梁先端の回転角、曲げモーメントが片持ち梁先端のたわみ量になります。

片持ち梁に等分布荷重が作用する場合

①：長さlの片持ち梁に等分布荷重wが作用しています。梁は一様断面で、ヤング係数および断面二次モーメントはそれぞれE、Iとします。

②：梁の任意の位置での曲げモーメントを算出するため、左端からxのところで自由体を切り出します。

③：x位置での等分布荷重の和が中心位置に作用するので、曲げモーメントはx²に比例します。

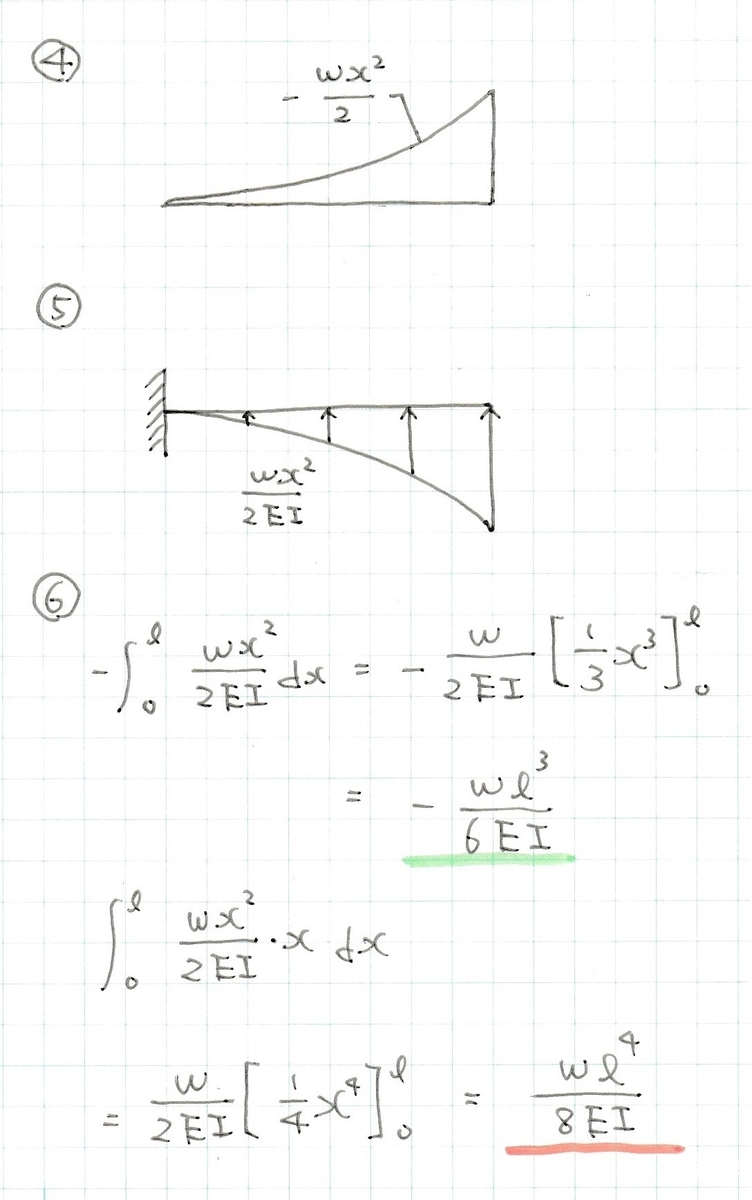
④：曲げモーメントは2次曲線状に変化します。

⑤：モールの定理に従って、左側の自由端を固定端に、右側の固定端を自由端に、モーメント分布を上下ひっくり返しEIで除して分布荷重に置き換えます。

⑥：分布荷重を積分することで固定端のせん断力を求めます。また、分布荷重にxを乗じたものを積分することで固定端の曲げモーメントを求めます。このときの固定端のせん断力が片持ち梁先端の回転角、曲げモーメントが片持ち梁先端のたわみ量になります。

単純梁中央に集中荷重が作用する場合

①：長さlの単純梁の中央に集中荷重Pが作用しています。梁は一様断面で、ヤング係数および断面二次モーメントはそれぞれE、Iとします。

②：曲げモーメントは直線状に変化し、中央で最大のPl/4になります。

③：モールの定理に従って、モーメント分布を上下ひっくり返しEIで除して分布荷重に置き換えます。単純梁では支持条件の変更は必要ありません。

④：分布荷重の面積を計算して2で除したものが反力です。反力が端部のせん断力、つまり単純梁端部の回転角になります。

⑤：梁の中央での曲げモーメントを算出するため、左側半分を自由体として切り出します。反力は④で求めています。

⑥：分布荷重の面積を計算して集中荷重Pl²/16EIに置き換えます。作用位置は三角形の重心位置です。

⑦：曲げモーメントの釣り合いから単純梁中央の曲げモーメントを求めます。このときの曲げモーメントが単純梁中央のたわみ量になります。

単純梁に等分布荷重が作用する場合

①：長さlの単純梁に等分布荷重wが作用しています。梁は一様断面で、ヤング係数および断面二次モーメントはそれぞれE、Iとします。

②：梁の任意の位置での曲げモーメントを算出するため、左端からxのところで自由体を切り出します。反力は等分布荷重に梁の長さを乗じたものの半分です。

③：x位置での等分布荷重の和が中心位置に、反力が端部に作用します。

④：曲げモーメントの釣り合いから任意の位置での曲げモーメントが求まります。

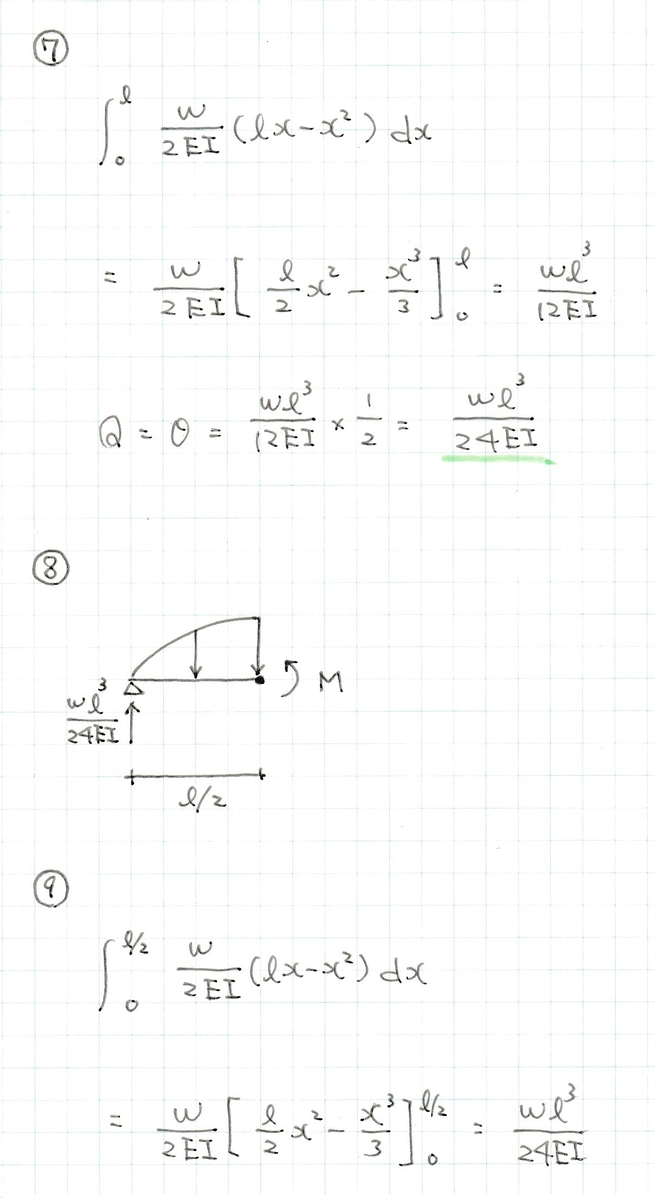
⑤：曲げモーメントは2次曲線状に変化し、中央で最大のwl²/8になります。

⑥：モールの定理に従って、モーメント分布を上下ひっくり返しEIで除して分布荷重に置き換えます。単純梁では支持条件の変更は必要ありません。

⑦：分布荷重を積分して2で除したものが反力です。反力が端部のせん断力、つまり単純梁端部の回転角になります。

⑧：梁の中央での曲げモーメントを算出するため、左側半分を自由体として切り出します。反力は⑦で求めています。

⑨：分布荷重を積分して集中荷重wl³/24EIに置き換えます。⑦で求めたせん断力の値と一致しますので、本来は計算する必要はありません。作用位置は分布荷重の重心位置です。「分布荷重にxを乗じて積分した値」を、「分布荷重を積分した値」で除すことで重心位置5l/16が求まります。

⑩⑪：曲げモーメントの釣り合いから単純梁中央の曲げモーメントを求めます。このときの曲げモーメントが単純梁中央のたわみ量になります。