断面二次モーメントと断面係数の計算：長方形・三角形・円形の公式を導出

建築の分野で使用する部材の断面は「長方形」か「H型」である場合が大半です。「H型」は「長方形」の集合であると考えることができるので、基本的には「長方形」に関する公式を暗記していれば問題ありません。

ただ、大学の講義やテストでは三角形や円形についても取り扱います。「公式の導出をしなさい」と言うのはよくある問題です。

ここでは断面の特性を表す代表的な値である中立軸回りの「断面二次モーメント」と「断面係数」の求め方を、順を追って解説していきます。

数式が苦手な方はこちらを先に読むとよいかもしれません。

断面係数と断面二次モーメント：梁せいの2乗・3乗に比例する理由

長方形の断面二次モーメントと断面係数の求め方

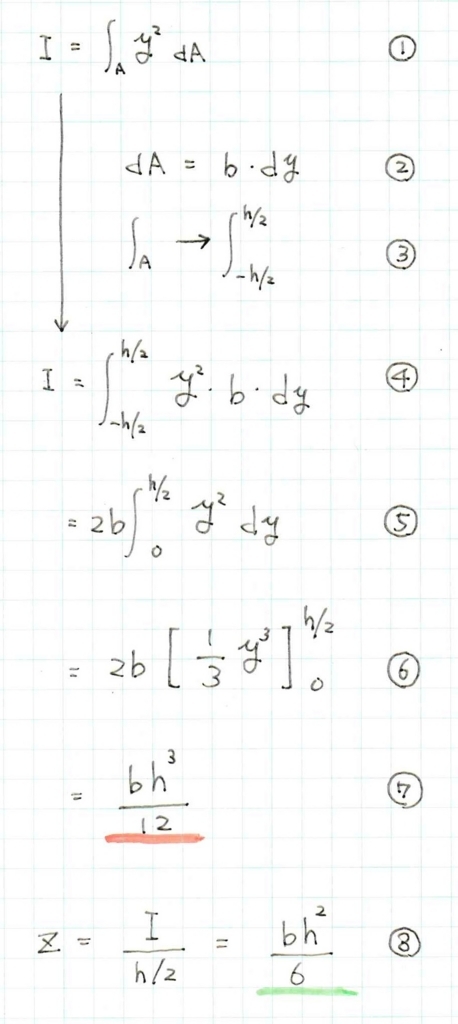
①：断面二次モーメントの定義式です。中立軸から梁せい方向に離れた距離yの2乗を全面積分集めなさい、ということです。

②：微小な面積dAは、微小な間隔dyに梁幅bを乗じたものです。

③：全面積分を集めるには、梁せいの下半分から上半分まで集めればいいです。

④：①に②、③を代入しています。

⑤：y²は偶関数（y=0に対して対象）なので、上半分×2でも同じ値になります。

⑥：y²を積分するので係数が1/3、乗数は3になります。

⑦：無事、見覚えのある長方形の断面二次モーメントの公式が導出されました。

⑧：中立軸（y=0）から断面の一番外側までの距離で断面二次モーメントを除せば、長方形の断面係数になります。

三角形の断面二次モーメントと断面係数の求め方

①：断面二次モーメントの定義式です。中立軸から梁せい方向に離れた距離yの2乗を全面積分集めなさい、ということです。

②：長方形と違い、梁の幅が位置によって直線的に変化します。中立軸位置では底辺の幅の2/3しかなく、最上部でゼロになります。

③：微小な面積dAは、微小な間隔dyにy方向の位置に応じて変化する梁幅b(y)を乗じたものです。

④：全面積分を集めるには、三角形の下から上まで集めればいいです。

⑤：①に②、③、④を代入しています。

⑥：y²を積分すると係数が1/3、乗数は3、y³を積分すると係数が1/4、乗数は4になります。

⑦：無事、三角形の断面二次モーメントの公式が導出されました。同じ幅、同じ梁せいであれば、長方形の1/3になることがわかります。

⑧：中立軸（y=0）から断面の一番外側までの距離で断面二次モーメントを除せば、三角形の断面係数になります。断面係数は長方形の1/4しかありません。

円形の断面二次モーメントと断面係数の求め方

円形の場合、XとYの「縦横」で表すよりも、Rとθの「半径と角度」で表す極座標の方が取り扱いやすいです。左側が円形断面の全体図、右側が拡大図です。

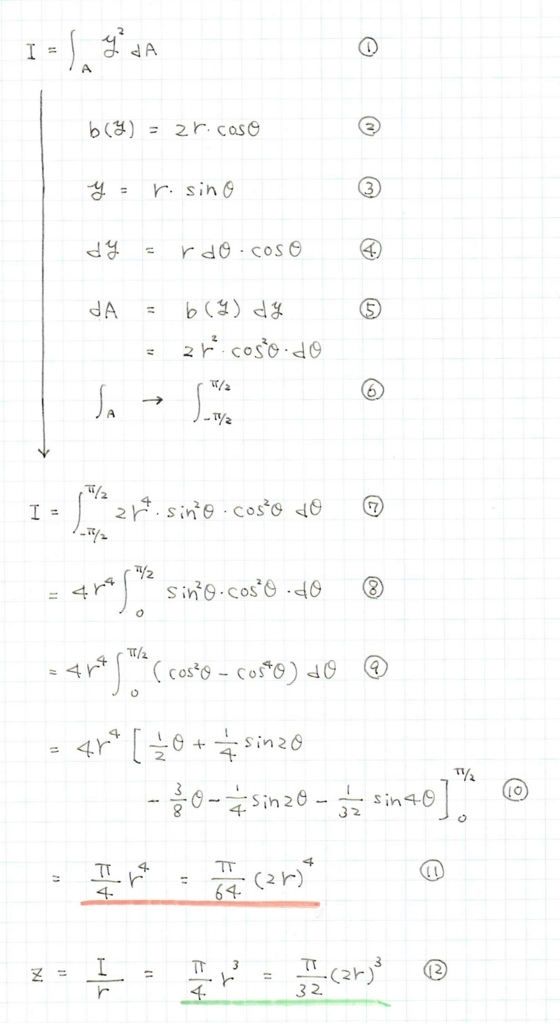
①：断面二次モーメントの定義式です。中立軸から梁せい方向に離れた距離yの2乗を全面積分集めなさい、ということです。

②：任意の位置yでの梁幅は、直径のcos成分で表すことができます。

③：任意の位置yを角度と半径で表すと半径のsin成分で表すことができます。

④：微小な間隔dyは少しわかりにくいです。拡大図をよく見てください。微小な角dθ間の円周は半径に微小な角を乗じた値r・dθになります。そのcos成分が微小な間隔dyです。

⑤：微小な面積dAは、微小な間隔dyにy方向の位置に応じて変化する梁幅b(y)を乗じたものです。

⑥：全面積分を集めるには、円形の下半分から上半分までの角度で集めればいいです。

⑦：①に②から⑥を代入しています。

⑧：sin²θ、cos²θともに偶関数（y=0に対して対象）なので、上半分×2でも同じ値になります。

⑨：sin²θ=1－cos²θの公式を用いています。

⑩：cos²θおよびcos⁴θの積分の公式を用いています。詳しく知りたい方は検索してみてください。

⑪：無事、円形の断面二次モーメントの公式が導出されました。同じ幅の正方形と比べると60%弱になります。直径の88%の幅がある正方形と同じ、とも言えます。

⑫：中立軸（y=0）から断面の一番外側までの距離で断面二次モーメントを除せば、円形の断面係数になります。